物理系统的动力学可以使用微分方程来描述。

       传递函数（TF）可以用拉普拉斯算子表示，这有助于理解其特性。每个传递函数都具有时域和频域特性，时域对应阶跃响应，频域对应幅频特性。

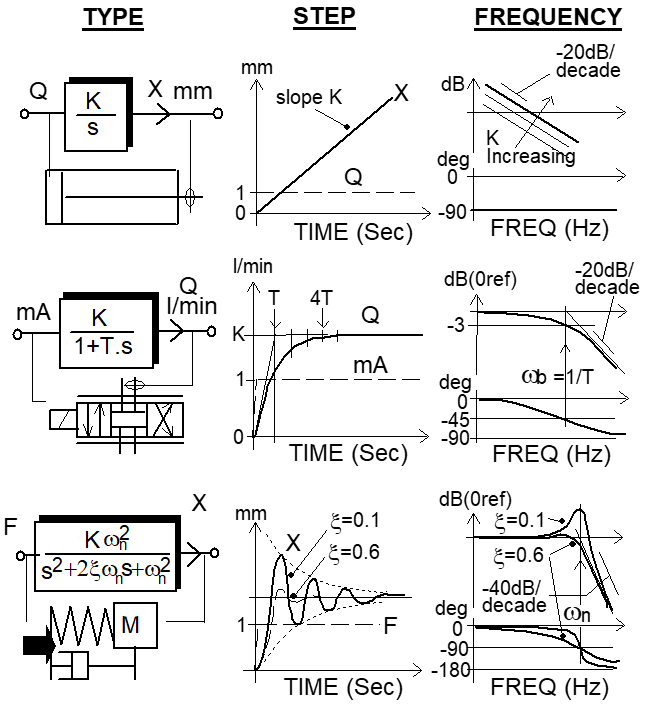
       例如，积分环节的传递函数为 TF(K)，其中 K 是增益。当单位油缸进油量为 K mm/s 时，油缸进油会产生速度特性（v = Q/A），但对位移而言，这是积分过程。速度的积分就是位移。阶跃响应在输入指令为0时停止，频率随增益以-20dB/dec的频率衰减，相位滞后始终为-90°。这是积分环节的典型伯德图特征，具体推导可参考《自动控制原理》。

一阶传递函数 TF(K, T)，其中 K 是增益，T 是惯性环节的周期。

       例如，当伺服阀的指令输入为 mA 时，输出流量将以指数方式上升至 K l/min。此时，伺服阀等效为一阶惯性环节。阶跃响应的初始斜率为 K/T，在 4.T 之后达到稳态值。频率和带宽分别为 -3dB 和 45°相位滞后为 1/T（弧度/秒）。角频率为 1/T 时，惯性环节会出现转折频率，即幅值显著下降的点，以-20dB/dec 的斜率下降。

二阶传递函数 TF(K, kesi, wn)

       其中 K 是弹簧系统的刚度，kesi 是衰减阻尼系数，wn 是系统震荡的固有频率。例如，一个典型的二阶震荡系统由单位质量/弹簧组成。在外部力的驱动下，其系统震荡的固有频率为 wn，衰减阻尼系数为 kesi，kesi = (K/m)^1/2。在液压系统中，K 是容腔的刚度。90°相位滞后出现在 wn 处，但实际峰值 dB 频率出现在低于 wn 的某个频率上，具体取决于阻尼系数 kesi。对于过阻尼的情况，即 kesi > 0.7，不会发生 dB 过冲。过冲是指谐振峰值，对应着阶跃响应中的超调。

注意：

1.一个系统的传递函数，可以将每个环节的物理方程写出来，然后换算成拉普拉斯算子，最终可以求得整个系统的传递函数TF；或通过最小二乘法直接拟合测得的阶跃和/频率响应数据。(注：这种方式是将整个系统看作黑匣子，根据阶跃响应和幅频特性数据，利用最小二乘法直接拟合，也可以拟合为三次或者更高层次的曲线。EXCEL表格就可以拟合)。

       后者通常用于从样本中获得简单的伺服阀模型。一阶和二阶模型均可用于表示伺服阀。这个主要看系统的带宽。如果伺服阀的带宽高于系统的五倍以上，可以将伺服阀等效为一阶系统，如果伺服阀带宽为系统的3-5倍，可将伺服阀等效为二阶系统。

2.完整的系统可能需要大量的传递函数来表示动力学。这需要按照系统的先后顺序逐个求出每个环节的传递函数，然后组合起来。这样系统将会非常复杂。例如，阀控缸的模型将是四阶的。这非常复杂，也没必要。